Sunday, August 27, 2006
Wisdom’s End

As you are aware, one of the goals of this blog is to explain how, in the modern era, we have ended up with two separate and in many cases diametrically opposed disciplines that claim to expand human understanding. Thus far we have shown that with the ancient Greeks, the two were for the most part still considered one. In contrast to this, we have found that by Newton's time, that the two have for the most part had become separate. Therefore, we can surmise that the shift occurred between these two periods. So perhaps we should then look to what has happened in between. As we know the civilization that in effect absorbed and then for the most part adopted that of the Greeks, was the Romans and their empire. The Roman empire initially began by first conquering the Greeks and thereafter in essence took for there own both their philosophy and religion. The Romans however were more ambitious as to their acquisition of influence and thereby territory. To aid them in thier endeavor, they employed Greek science put into practice to facilitate this.
Science, put into practice in the modern definition is technology. Now the narrow view of technology, is thought by many, to be simply engineering. Which is often in turn described as applied science. I submit that in the Roman case and even more poignantly our own, this is far too narrow a view. I would contend that when science is considered to be the practical basis for ones society, it tends to effect and hence shapes all aspects of human endeavor. Now for the Romans, at the outset, they incorporated the Greek ideas in a more holistic sense, as the Greeks themselves had for the most part. Where the expansion of human understanding was taken in the spirit of the exploration of nature and its design, as to how it applied not only to man, but the world as a whole. From this perspective they could form their society on what could be perceived as natural principles. The Greeks viewed things from the perspective of introspection, where this introspection would lead to virtuous individuals that would then form themselves into a thus virtuous society or state. Socrates often was contended to have proclaimed:
"Know thyself,"To extend this in terms of society as a whole he was known to insist:
"the unexamined life is not worth living."At the beginning with the adoption of these ideas, the Romans, more or less, mirrored the aspirations of the Greeks. However, later on, when ambitions for Rome extended beyond the Greek concept of city state, to expand to empire, the view and therefore the methods changed. along with the course and thereby the destiny of their society. To accomplish this expansion, the Romans turned away from the Greek ideals that philosophy served to expand the understanding of nature, to focus more on its practical application, in the service of man. Also, what started out as the semblance of a democratic social order, in the service of its citizenry, transformed into a dictatorial system, in the service of empire building. This in turn, inevitably lead to forces of discontent from both inside and out to question the basis of the very authority of Rome. One of these primary forces were manifest in a new emerging philosophy and that was Christianity. In the spirit of the history of Rome when they found one could not destroy a thing, one then incorporates it. This was the case with Christianity. At first emperor Constantine admitted its followers freedom of practice, returned confiscated property and gave land and tax free status to the new founded church. Later emperor Theodosius made it the official religion and banned all others with the closing of what he declared the pagan temples. The last stroke was that of emperor Justinian, in 529 A.D., with his order closing the last of the Greek schools of philosophy at Athens and the banning of such studies.
So how, you might ask, did this act to serve Rome or rather its rulers? From my viewpoint, forces inside the empire started to question the authority of the emperors. For it did not appear to serve the people, as it had once with the long past democratic system. This authority was brought further into question, since the new budding philosophy professed the equality of all men in the eyes of their creator. How then were the rulers going to maintain control in the face of this? The solution, adopt the new philosophy, bane the others and thereafter claim that their authority was given to them by this new God himself. This concept which became tradition has continued to this day and has even been incorporated into the newly created democracies in one guise or another.
Now I don't want you to take me wrong, for I have no political agenda in all this. Nor am I attempting to lay blame on the Christian or any other related philosophy. My sole intent is to set up the context and background as to how and why this split occurred between science and philosophy. For what I contend is, that with the banning of Greek philosophy and methods, for political ends, is what effectively began the then slow process as to what manifested itself into the roles of science and philosophy as observed today. Essentially, this policy, at first halted the expansion of understanding, in philosophic terms, as defined by the Greeks and along with it much of the knowledge gained. Also, it created a tension that would force any new emergence of renewal of such, to avoid conflicting with the new religious philosophy, in terms of its authority. Primarily what I'm referring to, is any aspect that might serve to address the question "why", beyond what this new philosophy so dictated.
In future posts, we will expand on all this, to discover how this new face of science emerged in the early years. We will also find, that ironically the very philosophy that in effect became the instrument used (or more properly misused), as reason to banish the old philosophies became the depository and keeper of this then forbidden wisdom. We will learn of the early practitioners, as to from whence they came and what they did in terms of expansion of human understanding. We will discover the limits placed on them and how this in turn served to shape our modern concept of science. However, for now all of this must wait to be explained in upcoming entries.
Friday, August 18, 2006
Cycle and Epicycle, Orb in Orb
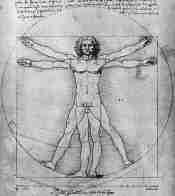
In the course of this blog, I have been speaking about this contention of mine, that the split between science and philosophy is focused around who addresses the “how” questions and who deals with the “why” ones. I’ve shown that for the most part, science sticks to “how” and leaves the “why” to philosophy. Lately, in particular, I have been speaking about the scientific method, as to what it contains or allows, as well as what it does not. One of the key elements of the method, is the use of mathematics. Now as we know one of the most basic tools in science, is mathematics. In fact many mathematicians would claim that it is the most fundamental of the sciences, rather then physics. There are others that would say that mathematics is not a science at all, but rather a hybrid of logic. However, the purpose of this post is not to enter this debate. What I would like to talk about is how mathematics itself, to a large extend, mirrors the rest of science in the context of how it forms our attitudes in regards to the discovery of truth in the natural world. To be fair I should say our common view. The example I will use to expand on all this is a mathematically defined shape that all of us are familiar with and that is a circle.
Now to begin, if I asked you to describe a circle, what comes to mind? This would seem to be a easy question, yet if I were to take to the street and solicit answers from a cross section of the populous, I suspect I would get a variety of replies. Some might say, it’s the shape we see when we look at a wheel. Others might say it’s the shape we see when we look at the moon or the sun. The more scientific might give a explanation that is somewhat more technical. In general though, I would suspect that most people would draw on things found in nature or constructed by man to describe it. This said , I would also wager that when you think of a circle, you see it in the abstract, as to what it is without reverence to any physical object. Now if you were to look for a formal definition, what would you find? Well I looked to many sources, including several dictionaries. For instance in all dictionaries I referred to, the one given was almost identical to the following, stated in Webster’s online dictionary as:
"a closed plane curve every point of which is equidistant from a fixed point within the curve"For a more professional definition one might refer to Wolfram’s Math World (a site I highly recommend), yet in this case it states much the same:
"A circle is the set of points in a plane that are equidistant from a given point."Now what is the difference between what many of you describe or only hold in your mind and what we find here as a definition. The difference is, in your mind, you hold it as a preformed thing, in its completion or “what” it is. In the definition, what is being described is “how” it is, as to how you would go about constructing a circle. Like the task performed when you use a compass to create one. This definition also, in a indirect way,both implies and relies on another abstract concept and that is the one of infinity. For the points described must be both infinite in number and have no space between them, otherwise one ends up with something that although circle like, would still not be a true circle. So is there another way to describe a circle, which does not rely on a reference to other objects or ill defined abstract concepts?
Before I reveal this other way to describe a circle, let’s first review what I told you were the key “hunches” that science uses to find truth in the natural world. There were two. One was economy and the other was symmetry. Now let’s suppose that we are nature. In this case I will limit us to be nature of a two dimensional world. That is, one that is restricted to a plane or flat land. Now let’s suppose, we as nature, constructed this world to comply with these hunches I pointed out. So if we imposed these hunches as our rules to make real, a basic and fundamental shape for this universe, what could be one that we would end up with? Okay, let’s imagine we say we want a two dimensional form, that always is in proportion, a line of least length to enclose the greatest amount of area . For as I said, we are nature and so therefore we want our basic structures economical in both form and explanation. So what form would we have thus just demanded? Well as I think you will have guessed, if you didn’t know already, it is the circle. Now what about the symmetry part? Remember we defined symmetry as when one takes a thing and does something to it in regards and respect to the allowed levels of freedom (dimensions) and it there after remains unchanged. What can we do to the circle to see if it has symmetry? First, we could just move it around our two dimensional universe. When we do this, ( to no great surprise) no matter to what distance moved, it still remains the same in both form and function. Now what if we rotated it as allowed in this universe, will it change? No it will not. So now we have found by invoking this rule of economy, we have in turn ended up with something that also demonstrates symmetry. Now you might retort, that’s fine for this mystical flat land, but what of the real world. In response, I would remind you that the three dimensional projection or analogue of the circle is the sphere. The sphere described in the way I have just shown, would be a form that always is in proportion the surface of least area enclosing the greatest amount of volume. The economy here is also evident and the tests we imposed to confirm symmetry, would hold the same.
Now you say, so what, for the objects just described are simply abstractions. You continue by insisting they are therefore forms only created in our minds. You could thus feel this should end it all. That would be true, if the circle and its somewhat distorted cousin the ellipse were not so prominent in both the form and action of our natural world. That it is to say, it has proven to thereby have purpose. The other way to state it is, “why” is the circle (or the sphere)? The answer of course is to have a entity(s) that can act in purpose that is both economical and symmetrical in form and function. I thus find it unfortunate, that although science looks to these hunches to discover truth of the world, that it at the same time denies the “why”, that also lends insight into not only the means of it’s construction, but also of its utility.
In summation today, I would bet in the beginning, when I mentioned mathematics many of you thought, oh no, here come the formulas and equations. In contrast to this expectation, as demonstrated above, many might be surprised to find that if they explored both mathematics and science, at the more fundamental level, you may discover it to be simple, beautiful and yet excitingly mysterious. I would ask now, the next time you are given to describe a circle, what will be your reply?
As a foot note to this, let me leave you with a quote from Milton’s “Paradise Lost” that I find projects the spirit of what I have attempted to convey:
From man or angel the great Architect
Did wisely to conceal, and not divulge
His secrets to be scanned by them who ought
Rather admire; or if they list to try
Conjecture, he his fabric of the heav'ns
Hath left to their disputes, perhaps to move
His laughter at their quaint opinions wide
Hereafter, when they come to model heav'n
And calculate the stars, how they will wield
The mighty frame, how build, unbuild, contrive
To save appearances, how gird the sphere
With centric and eccentric scribbled o'er,
Cycle and epicycle, orb in orb.
Saturday, August 12, 2006
Reason Denied

With my last post I spoke of Francis Bacon and the mark he left on modern science with his method. I also pointed out, how this proposed method was later championed by none other than Isaac Newton. Further, it was indicated that the base premise of the method, is that there was not to be taken anything that could be considered as a preconceived truth or foreknowledge as a premise. In so that, the only things that could be used as such, where those that had been established by inductive reasoning suggested and confirmed through methods of experimental observation. What I also demonstrated was that this method denies that man has the capacity to know anything that is simply a given despite what I had shown earlier, that science truly could not function without such notions. At the conclusion, I stated there were those, that have denied this program to some extent to contest there are things that we simply know which can be used within the context of “why”, to further our understanding of the world. One such person was René Descartes (1596-1650)
René Descartes was a philosopher, mathematician and physicist. His obvious and best known contribution to mathematics and thereby science is in the founding and development of what is referred to as analytical geometry. This of course is the considering of geometry in the back drop of algebra. It also in turn lends algebra spacial qualities. What many of us, are most familiar with in this regard, is the plotting of algebraic formulas in as to represent space plotted in relation to defining number lines. These are of course known as Cartesian coordinates, named in his honour. This also formed the foundation from which Newton and Leibniz later created calculus. Now if this were not enough, Descartes is also considered the founder of modern philosophy. On the subject of Descartes and philosophy, I will speak in more depth in future posts. For now though, I would like to focus on his thoughts of what the expansion of knowledge should be in terms of science and the method it should follow.
Descartes, as Bacon, was suspect and concerned about what could be considered true. However, in contrast to Bacon, Descartes insisted that deductive rather than inductive reasoning should serve as the base logic for the scientific method. Now this deductive process wasn’t that of the then common type, where one could declare just about anything as the base premise or axiom in terms of what is then to be considered and thus deduced. To illustrate more clearly what form this took, I quote here from his paper entitled, Discourse on The Method: of Rightly Conducting The Reason, and Seeking Truth in the Sciences (1637)
“Among the branches of philosophy, I had, at an earlier period, given some attention to logic, and among those of the mathematics to geometrical analysis and algebra, -- three arts or sciences which ought, as I conceived, to contribute something to my design. But, on examination, I found that, as for logic, its syllogisms and the majority of its other precepts are of avail- rather in the communication of what we already know, or even as the art of Lully, in speaking without judgment of things of which we are ignorant, than in the investigation of the unknown; and although this science contains indeed a number of correct and very excellent precepts, there are, nevertheless, so many others, and these either injurious or superfluous, mingled with the former, that it is almost quite as difficult to effect a severance of the true from the false as it is to extract a Diana or a Minerva from a rough block of marble.”Here we discover that Descartes, much like Bacon, was concerned with what could be considered true. In the next quote he states that he was in search of a method for science that would contain reliability and precision for he says:
“I was induced to seek some other method which would comprise the advantages of the three and be exempt from their defects.”So what Descartes has said is that although there is much that is true in what he considered the somewhat unreliable sciences, he needed to find a method by which the reliability and thus the utility of science could be improved. To begin he lays out his method in four parts, the first being as follows:
“The first was never to accept anything for true which I did not clearly know to be such; that is to say, carefully to avoid precipitancy and prejudice, and to comprise nothing more in my judgement than what was presented to my mind so clearly and distinctly as to exclude all ground of doubt.”Here as Bacon had stated, all should be considered with the element of doubt, where nothing can be simply taken as a given. However, unlike Bacon, Descartes has already suggested, that there are some things that by there very nature can be taken as true. He also suggests that this judgement is to be found within ones self and not externally. Something that I would view as almost considered instinctive reason, for lack of a better term. The next step he states as:
“The second, to divide each of the difficulties under examination into as many parts as possible, and as might be necessary for its adequate solution.”Here again, just as Bacon had insisted, things must be first broken down into all things that might be considered. Now Descartes next step is explained in the following.
“The third, to conduct my thoughts in such order that, by commencing with objects the simplest and easiest to know, I might ascend by little and little, and, as it were, step by step, to the knowledge of the more complex; assigning in thought a certain order even to those objects which in their own nature do not stand in a relation of antecedence and sequence.”Still from what has been said, the methodology of Bacon and Descartes are looking pretty much the same as Descartes says that not only should ideas be broken down into the smallest parts possible. He futher suggests they be assigned order, whether or not they at first appear to have priority of importance or that of connectivity of structure. He is talking about acending in small steps, which would normally relate to a bottom up approach, which on the face of it looks like a inductive process. He completes his four steps with the following:
“And the last, in every case to make enumerations so complete, and reviews so general, that I might be assured that nothing was omitted.”Now at this point you may be confused, as to why I consider there is a distinction to be made between Bacon and Descartes in terms of their methods. From what has been revealed up to now, it appears that Descartes is just restating what Bacon said some 17 years prior, without perhaps the mention of observation, although it has not been excluded. It also seems to be shaping up to be performed within a inductive frame work, that would be satisfied as in Bacons method, only through exhaustion. But now in the following we find that the system of reasoning that Descartes insists to be primary in its execution, is not induction at all, for he now states;
“The long chains of simple and easy reasonings by means of which geometers are accustomed to reach the conclusions of their most difficult demonstrations, had led me to imagine that all things, to the knowledge of which man is competent, are mutually connected in the same way, and that there is nothing so far removed from us as to be beyond our reach, or so hidden that we cannot discover it, provided only we abstain from accepting the false for the true, and always preserve in our thoughts the order necessary for the deduction of one truth from another.”Despite the similarity in the preamble, we now discover, that what Descartes has in mind as the principle method of reasoning, is that of deduction and not of induction. It's not hard to imagine why Descartes feels this way, for as I mentioned before and he himself here eludes, that he was also a great mathematician. Mathematics in the main is a deductive process, building from what are referred to as axioms, that are used as premises, to deduce further truths. Bacon on the other hand, avoids for the most part this method and not surprisingly so, for he was not a mathematician as was Descartes. Bacons primary training and occupation, was that of a lawyer. In the few scientific explorations he did conduct, he excluded the use of mathematics almost entirely. I must also relate, that he had little success. Now that Descartes has set up this program of discovery, he finds himself with a bit of a dilemma, as now, what is he going to use as his axiom(s), to begin this step by step deductive process? After all, he has, as Bacon did earlier, dismissed all prior known truths. What then is he going to utilize as his foundation on which to build his deductive method? Here we now witness Descartes in his eureka moment, for he states;
“But immediately upon this I observed that, whilst I thus wished to think that all was false, it was absolutely necessary that I, who thus thought, should be somewhat; and as I observed that this truth, I think, therefore I am (COGITO ERGO SUM), was so certain and of such evidence that no ground of doubt, however extravagant, could be alleged by the sceptics capable of shaking it, I concluded that I might, without scruple, accept it as the first principle of the philosophy of which I was in search.”Now Descartes has discovered, his first and primary truth, from which he proposes that all the others will follow and in turn proved is to be, he “thinks” so therefore he “is”. He contends here he has found the bedrock truth that he feels that no one can dispute and that is they exist. This, like many other statements in history, have been repeated so many times, that they tend to become completely misunderstood. Some for instance imagine, that this means that only things that “think”, “are“. That is because many do not understand the deductive process, for they imagine that like a equation this suggests that (think = am). That would mean that to write (am = think) is the same. Now to compare, what if I said , I “walk” so therefore I “travel”. If this were then interchangeable, you could say, since I “travel” so therefore I “walk”. I don’t know about you, but I take the bus some times. Also, it could thus be suggested, that baseballs have legs. No, deductive reasoning is very precise, for it only holds that what is deduced from the premise is true, not that it is equal to the premise.
So now we have discovered, that Descartes has proposed a method, in which the deductive process serves as its primary system of logic. It must be also made clear that he does not entirely omit the inductive process, which in science is rooted in its observations. He however warns, that in these observations that deduction must also play a role for as he states:
“But this is certain, and an opinion commonly received among theologians, that the action by which he now sustains it is the same with that by which he originally created it; so that even although he had from the beginning given it no other form than that of chaos, provided only he had established certain laws of nature, and had lent it his concurrence to enable it to act as it is wont to do, it may be believed, without discredit to the miracle of creation, that, in this way alone, things purely material might, in course of time, have become such as we observe them at present; and their nature is much more easily conceived when they are beheld coming in this manner gradually into existence, than when they are only considered as produced at once in a finished and perfect state.”What Descartes is pointing out with this, is that to observe something as it is and then therefore suppose it is, as it was always, is a mistake. Therefore, one must also consider it may have come from something or things simpler perhaps and to look to this also as a possible explanation of outcomes in observation. He is saying that induction is therefore vulnerable with this flaw and it is only by deduction that we may be able to avoid this. What is also interesting to note, is that this is turn would later serve as the seeds of discoveries, such as Darwin’s. In as Descartes suggests with this, that the world is not so much a place of being, but rather a place of becoming, as to what it will be. It is of no wonder with such thoughts, that shortly after his death, the Vatican put some of his writings on the forbidden reading list.
Now once again we have come to the question, so what is my point? Actually I have a few. The first, is to indicate the differences between the methods of deductive and inductive reasoning, when used as science’s base. In the inductive process, where observation plays the primary role, truth is formed by consensus or the weight of evidence rooted in a statistical background. If all the available observations support a conclusion, then it is considered to be true. In the deductive process, truth is only established with reason derived from a premise, which is a self evident truth or has been before deduced from one. Both are processes that attempt to relieve doubt. However, in the inductive process, with nothing pre-established as truth, what is proposed is only as good as the observations taken and the methods so used to consider them. In deductive reasoning, everything is derived from the premise, the only remaining doubt is that of the soundness of the initial truth and the correctness of the connections made with subsequent deductions. In deduction, we must look to the premise and only that to be sure. In induction, we have to not only trust our observations, as to their quantity, but also the quality of them. It must be also assured that the inductive statement then formed is a strong one, in the context of the data collected. In the deductive process, the demanded first requirement is to initially ask “why”. To realize this, lets look to what Descartes must have done to come up with his initial premise. He would have had to at first asked, “why” am I certain that I “am“? His answer would then have followed because I “think”. With this one may see more clearly that the function of “why”, is to lend certainty to man's understanding and thereby of nature's, so that we might have firm footing to further explore its aspects of purpose and thereafter perhaps its utility, in concert with other means presented or at our disposal. This is what Descartes so discovered and which I most certainly agree is so.
As a post script to this, I would like to address as to what happened to Descartes ideas, in the context of their current application to science. Descartes today, is viewed as primarily a philosopher and by many a great one at that. He is not however, considered much as a scientist, despite the fact that he is also acknowledged as the founder and father of analytical geometry, that science still covets and from which also Newton required in the course of discovering calculus. I would contend, that not only for his refinement and promotion of this deductive method, which I have attempted to explain, but also stressing that the “why”, plays a role in understanding, that he was then so dismissed. As evidence of this, I will make one final quote. This quote is of Voltaire, who discussed in the following, just what I have contented. Here he is to be found using Newton as the comparison in this regard upon a visit to England in the mid 1700‘s. ;
We may admire Sir Isaac Newton on this occasion, but then we must not censure Descartes.
The opinion that generally prevails in England with regard to these new philosophers is, that the latter was a dreamer, and the former a sage.
Very few people in England read Descartes, whose works indeed are now useless. On the other side, but a small number peruse those of Sir Isaac, because to do this the student must be deeply skilled in the mathematics, otherwise those works will be unintelligible to him. But notwithstanding this, these great men are the subject of everyone's discourse. Sir Isaac Newton is allowed every advantage, whilst Descartes is not indulged a single one. According to some, it is to the former that we owe the discovery of a vacuum, that the air is a heavy body, and the invention of telescopes. In a word, Sir Isaac Newton is here as the Hercules of fabulous story, to whom the ignorant ascribed all the feats of ancient heroes.So to conclude, I would submit, that the fear Voltaire expressed as to the fate of Descartes and thereby his ideas, has come to pass. It is then not to wonder, why, lesser persons choose not to follow the route of Descartes, but rather that of Newton's, to avoid such. This then is not to say that no one has since. As there have been a few. These few in turn, have also broadened the insight of humanity and yet as Descartes, have in there own way also been made to pay the price. About these people and other related things I will continue to speak of in future posts.
Saturday, August 05, 2006
The Dawn of Reason?

It has been about a week since my last entry. The longest stint since beginning this blog. You have my apologies for this, yet it seems whenever I turn my thoughts to the subject of time, as I had in my last post, it sets my head into a protracted wonder mode. When this happens all other thoughts seem to end up on the back burner. With this said what it is I’d like to return to today, is this subject of “how” and “why” this split between science and philosophy occurred. When I last addressed this I was speaking of Newton and what his thoughts on the expansion of human understanding and it’s methods were. What we discovered was although Newton was certain there was a underlying scheme to nature, he was also equally certain, that asking the “why” question would not serve to help discover it. Basically what he thought is as many do today, that science will only extend human understanding by focusing on the “how” questions, through what he indicated was already a predescribed method. He synopsised this method as you recall in saying:
This on the face of it looks like a very straight forward statement. However, if examined more closely you find it to be something quite complex. The first thing that could be misunderstood is perhaps the only system of logic that is utilized by the modern science is that of induction. One also has to understand that this induction is not of the common type, for it would be better described as induction through exhaustion. This is what I previously described as the “typing monkey method”. Let’s first take a definition of inductive reasoning from Wikipedia:“In this philosophy particular propositions are inferred from the phænomena, and afterwards rendered general by induction.”
Now as many of you know, inductive reasoning, while useful, has the central flaw of not on its own being all that reliable. Also, inductive statements are further categorised generally into two types, which are “strong” and “weak”. An example of a strong inductive statement would be, “ all observed polar bears are white so therefore all polar bears are white”. The first problem here is that it is assumed that every polar bear has been observed and of course that is not the case. The second is if we find a bear that is say, black instead of white, although living in the artic, does this mean therefore it is not a polar bear. The weak inductive statements can pose even greater difficulty. An example of this might be, “ All my pants have zippers so therefore all pants have zippers". I don’t think I need to point out where the fault is with this. So now one might assume that the whole method could be flawed if solely dependant on induction. Happily it is not, for it also is dependant on what is called deductive reasoning. This however is not all that self evident in Newton’s statement, as it has been disguised or belittled somewhat as the word “inferred”. What then does “infer” mean. The Oxford defines it as “to deduce or conclude”. In the “Free Dictionary” its defined as “To conclude from evidence or premises”. So now let’s look at what deductive reasoning is. Again from Wikipedia they state:“Induction or inductive reasoning, sometimes called inductive logic, is the process of reasoning in which the premises of an argument support the conclusion but do not ensure it.”
Deductive reasoning is reasoning in which the conclusion is necessitated by previously known facts - the premises: if the premises are true, the conclusion must be true
So now then, how does this differ from the inductive method? As a example of a deductive statement one could assert," in as the polar bear is above the ice sheet, and since the ice sheet is above the earth, therefore the polar bear is also above the earth.". Now deductive process can also be flawed if the connection between what is considered the premise and what is deduced has not been truly established as a commonality. For instance I might say: All polar bears dislike the heat, I dislike the heat, so therefore I am a polar bear. In general, the process of deduction is dependant on first sighting self evident truths, so then if they are true so is your conclusion. As can be seen here, we have two systems, which in a sense could be considered diametrically opposed. Induction, were nothing is assumed true, nor can it be and deduction, where some things are taken as true by their nature or taken as a given. This is then what would appear to be two incompatible systems that science uses to expand its knowledge of the natural world.
But how can this be accomplished? Well the way this has been carried out for the most part is to minimize the use of the deductive process and when one cannot in some sense disguise it. The deductive process for the most part lay hidden from view to many inside what are its mathematical formalisms and also the hunches I have previously mentioned. The part that is there for all to see is the inductive process, were everything is suspect and nothing assumed. This is considered by many not only to be the core but also the strength of modern science.
So once again you might ask, how did we end up here? Now as I have relayed before, it is not something that appeared out of thin air. It is rather something that has occurred over the course of time within the context of certain events. What I can say is, that there was a time, a place and a person in which all this crystallized, to take what is for the most part its final form, as it is perceived today. The time was 1620. The place was London, England and that person was Francis Bacon. The crystallisation, as I have so called it, was with a paper I have before mentioned, entitled, “Novum Organum” or “New Instrument”, for those who were not required to study Latin. In this paper Bacon outlined and promoted a method by which he said man in general and science to be specific must follow, if it hoped to significantly improve human understanding of the natural world. Now I've considered the ways I might explain and portray the nature and focus of this document, for there appeared to be many. It then should be established that Bacon thought that the inductive method or what would be better expressed as Bacon's inductive process, is the meat of what he viewed as the true methodology for all of science. Let’s first confirm what Bacon had in mind as to the utility and scope of his proposed method. In the introduction of his treaties he states:
As one can see here Bacon had both great hope and aspirations for what he considered his new method. In fact, in some sense he was correct to make such a boast, for his method for the most part, still serves today as the blue print of science.“But if there be any man who, not content to rest in and use the knowledge which has already been discovered, aspires to penetrate further; to overcome, not an adversary in argument, but nature in action; to seek, not pretty and probable conjectures, but certain and demonstrable knowledge — I invite all such to join themselves, as true sons of knowledge, with me, that passing by the outer courts of nature, which numbers have trodden, we may find a way at length into her inner chambers.”
Now does Bacon stop at natural philosophy. Let’s quote him again from this document as he proposes the following:
Here we find that this method is proposed to govern and guide all mans conception and aspirations of truth along with its resultant considered actions. It could be argued that Bacon’s insight and ambition for the most part has held sway in terms of the form and condition of our society and its thinking. Now here you will find that Bacon held induction as the key and central tenet of this method. Now I quote him in as saying:“It may also be asked (in the way of doubt rather than objection) whether I speak of natural philosophy only, or whether I mean that the other sciences, logic, ethics, and politics, should be carried on by this method. Now I certainly mean what I have said to be understood of them all; and as the common logic, which governs by the syllogism, extends not only to natural but to all sciences, so does mine also, which proceeds by induction, embrace everything.”
Now for those who are not familiar with what the term “syllogism” , it refers in general to the whole method and practice of deductive reasoning. What he is contending here, is that deduction should not be trusted and only with inductive reasoning can be discovered what he insists to be reliable truth. What he calls “true induction” is a induction rooted in doubt and only satisfied through exhaustion. These are of course concepts which I have discussed in earlier posts. So what do I mean by exhaustive induction? Let’s see what Bacon thinks this should entail when he goes further in saying:“The syllogism consists of propositions, propositions consist of words, words are symbols of notions. Therefore if the notions themselves (which is the root of the matter) are confused and overhastily abstracted from the facts, there can be no firmness in the superstructure. Our only hope therefore lies in a true induction. “
"In establishing axioms, another form of induction must be devised than has hitherto been employed, and it must be used for proving and discovering not first principles (as they are called) only, but also the lesser axioms, and the middle, and indeed all. For the induction which proceeds by simple enumeration is childish; its conclusions are precarious and exposed to peril from a contradictory instance; and it generally decides on too small a number of facts, and on those only which are at hand”With this Bacon has proposed that all then givens along with all devices of deduction be discarded and replaced by only those discovered within the method of induction. You at this point could counter, how does this resemble our current method for where is the mathematics that is today so much a part of science? Here you will find your answer for he then states;
We have here found Bacon to make an exception to the deductive exclusion and that is in the acceptance of the deductive process when expressed through mathematics. For Bacon considers mathematics can be trusted to be part of the process. More specifically the equation. Now that sounds more like modern science doesn’t it.“the mathematical postulate that if two things are equal to the same thing they are equal to one another is conformable with the rule of the syllogism in logic which unites propositions agreeing in a middle term.”
Now I could go on for some time, discussing Bacon and his method in relation to the way we now endeavor to understand the world . However, on one hand I am fearful that I might in so doing, lose a couple of what as I perceive as my so few readers. Also, I would like to leave something for yourself on your own to discover or perhaps even find reason for you to take exception as to what I contend. However, before I put this to rest, let me quote Bacon once more, after which I will sum up. As my last quote Bacon writes:
What I would like to emphasize from this, is that Bacon himself admits and insists what I have claimed science views as the limit of human understanding. For Bacon tells us that man, has not the capacity to know anything as a given or a preconceived truth. Now in regards to this I must be honest and say I cannot take issue with him at all. For I surely do not know. What I do take issue with here I express within the following two points. First, as I have shown in earlier posts, science could not function at all without preconceived notions or considering foreknowledge of what is true. Not just in the mathematical sense, for which Bacon so graciously allows, but also in the more general case , which I have also previously demonstrated as the hunches that can be viewed as “qualities” of the general characteristics of nature. So in effect Bacon’s method and thereby that of science's is not executed as we perceive or as many of the vocation proclaim. My second and what I consider the most important point to be made, is that despite Bacon's premise and science in its practice, these have not served to demonstrate that the “why” questions of nature and its process, has no place in science or lacks ability to expand human understanding. Later in the course of this blog I will speak of those who broke Bacon’s and thus science's rules to not only ask the question “why” but also admit that they have. You may be surprised to discover who they are and what this has achieved.“To God, truly, the Giver and Architect of Forms, and it may be to the angels and higher intelligences, it belongs to have an affirmative knowledge of forms immediately, and from the first contemplation. But this assuredly is more than man can do, to whom it is granted only to proceed at first by negatives, and at last to end in affirmatives after exclusion has been exhausted.”

